Before we discuss the use of data windows, we should first remind ourselves of three basic properties of the FFT (Fast Fourier Transform) process.
- First, energy information in signal must be preserved during transformation. That is, the energy measured on time signal must equal the energy measured on the frequency representation of that signal.
- Second, an FFT converts the signal representation between time and frequency domains. The time domain representation shows when something happens and the frequency domain representation shows how often something happens.
- And finally, an FFT assumes that the signal is repetitive and continuous.
Let us consider an example. First, we will look at the special case of a 10Hz sinusoid (Figure 1). This signal is periodic within the time record used to calculate the spectrum.
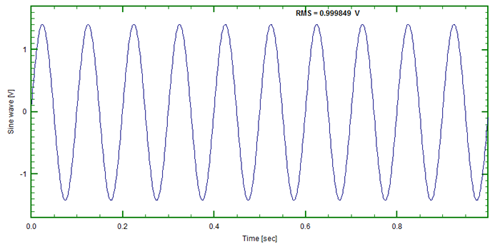
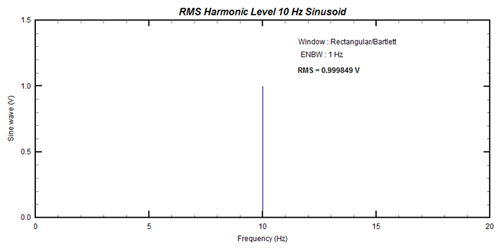
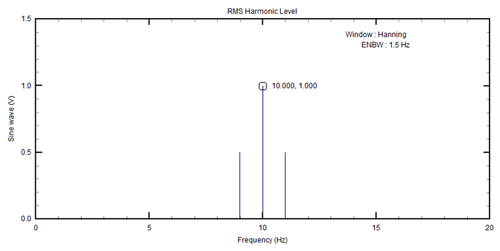
If we perform an FFT using the DATS software the result, shown below, will consist of a single line in the spectrum with an amplitude that represents the rms of the time series amplitude.
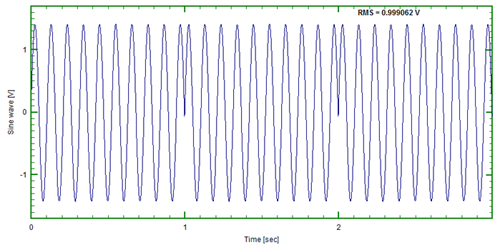
Now, let us consider a second example. In this case (Figure 3) we have a 9.5Hz sinusoid.
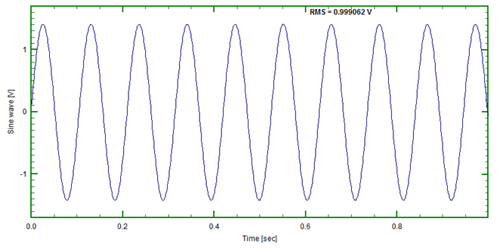
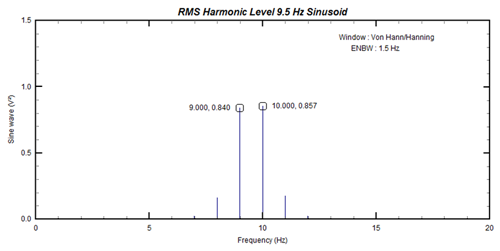
If we perform an FFT operation on this it yields the multi-line spectrum shown in Figure 4.
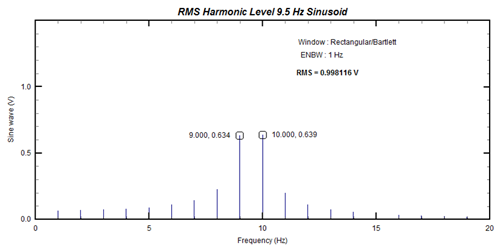
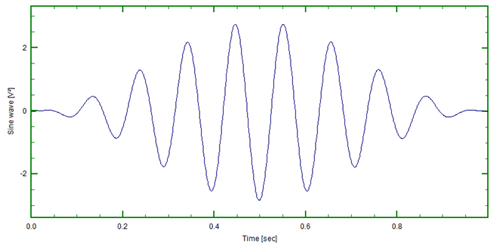
So why is it not a single line spectrum?It is still a sinusoid isn’t it? Well, not as seen by the FFT process. It assumes the signal to be periodic (not only within a single record) and on-going or continuous. The 9.5 Hz signal (Figure 3) seen in analog form is on-going and continuous, but when viewing it from a digital perspective (discrete number of samples in a specified time block), this signal is not a sinusoid (see Figure 5).

This is why the FFT produces the multi-line spectrum in figure 4 with up to 20 visible lines. Our next question is – How do we minimize the effects of the discontinuities? The answer is that we use something called a “window”. Typically, the window used for most general purpose data is the “Hanning” or “Von Hann”. In the DATS software it is called the “True Hanning” window.
The “Von Hann” or “Hanning” window is named after Julius Von Hann (1839-1921). Von Hann was an Austrian meteorologist and is seen as the father of modern meteorology. He was the director of the Central Institute for Meteorology in Vienna (1887-1897), professor of meteorology at the University of Graz (1897-1890) and professor of cosmic physics at the University of Vienna (1890-1910). In signal processing the Hann function was named after him by R. B. Blackman and John Tukey in “Particular Pairs of Windows.” published in “The Measurement of Power Spectra, From the Point of View of Communications Engineering”, New York: Dover, 1959, pp. 98-99.
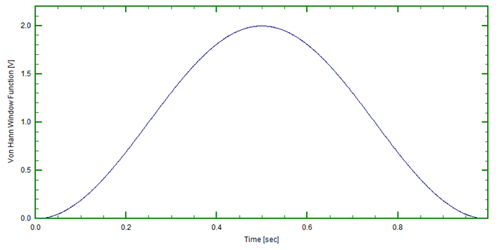
Multiplying the window function (Figure 6) by the original time signal forces the signal to zero at the beginning and end of each time record (Figure 7).Placing multiple time records shown end to end shows the signal is now forced to be periodic when the time records are placed end to end.One problem solved, but the signal now in each of the time records is not a sinusoid any longer.This modification to the sinusoid is represented in the frequency domain as 4 lines in the frequency representation of the signal.
The spectrum which was 20 lines before applying the Hanning Window function has now been reduced to a spectrum of only 4 lines.Not perfect, but much closer to the single line spectrum one would expect for the single frequency time signal. Obviously, one never get something for nothing.What happens to the single line spectrum from the 10 Hz single frequency time signal?Instead of a single line spectrum, the modified single frequency signal now is represented by a 3 line spectrum (Figure 9).There is no loss in amplitude read out accuracy, but a loss in frequency resolution is present.
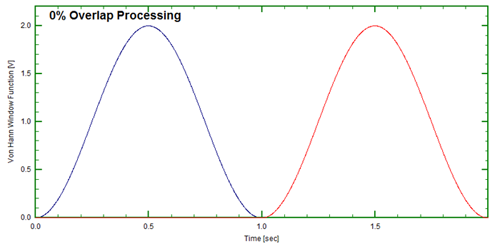
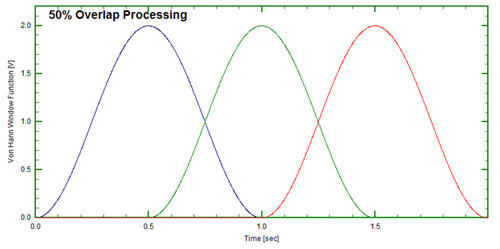
But what do we do about the data that is being missed at the beginning and end of each record? Data is being reduced and/or set to zero over one half the time record -How do we assure events happening in the region of reduced amplitude areas?A processing technique exists called “overlap” processing.By applying this technique, the events occurring at or near the beginning and ending of the time records are enhanced by using overlap processing. Figure 10 represents records being processed “end-to-end” or 0% overlap. Figure 11 shows overlap of 50%.
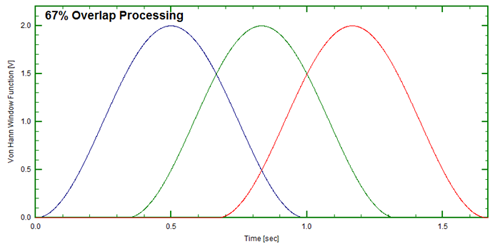
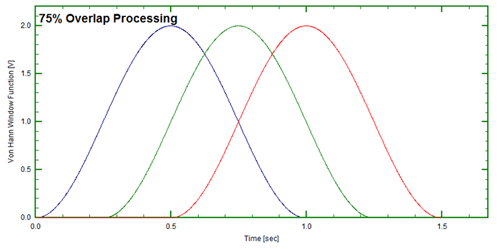
Typically 67% overlap (Figure 12) is considered sufficient to weight the events near the beginning/end of the time record, however 75% overlap (Figure 13) is somewhat better.Today, with the high processing capabilities of computers, there is little reason not to utilize overlap processing.
Different shapes of the windowing function dictate what the spectrum shaping looks like.The table below lists a few window function types. All Window functions that operate on the time domain signals typically zero out the beginning and end of time record. The obvious exceptions to this are the “force” and “exponential decay” windows used in hammer/modal applications.
| Type | ENBW | Amplitude | When to use |
|---|---|---|---|
| Rectangular | 1.0 | ~4 dB | Only when signal is known to be periodic within time record |
| Hanning | 1.5 | ~1.5 dB | Most often used general purpose |
| Flat top | 3.8 | <0.02 dB | When absolute amplitude accuracy is required – calibration/sensitivity check |
| Kaiser-Bessel | 1.8 | ~1 dB | When relatively high amplitude accuracy and frequency resolution important |
This article was originally created for a presentation to a North American Prosig User group (PUG).
Information on Julius Von Hann was taken from Julius Von Hann – Wikipedia, the free encyclopedia
John Mathey
Latest posts by John Mathey (see all)
- Exhaust Vibration Measurement – A Case Study - March 11, 2016
- What Is Amplitude Quantization Error? - January 27, 2016
- Creating An End of Line Vibration Test System - February 25, 2015


what does ENBW mean?
A very good question, Terry. Something we should have expanded on on the article perhaps. We have a related article that will appear on the blog in the near future that deals with this in a bit more detail. But for now, ENBW stands for “Equivalent Noise Bandwidth”.
If windowing in time domain have purpose to get more accurate representation in frequency domain (depending on the characteristics of signal in time domain as mentioned in this article), so is there any purpose by windowing the spectrum or frequency domain?
Suwarnov, a very interesting and profound question. Colin Mercer, our Chief Technical Officer has provided a response to your question.
John Mathey
– – – – –
When we measure a finite length of data then we will always have a data window, by default the rectangular window. In fact we call it a window as the section of the signal we measure is like looking at the world through a window; we do not know what is happening outside the part we have measured (observed). What we measure is represented mathematically as the product of the actual signal multiplied by a rectangular window that is zero before and after our measurement and unity during the measurement time.
When the measured time signal is converted to the frequency domain by a Fourier transform then we have not actually gained or lost any information as the Fourier transform is totally reversible. What we have done is represent the signal in a form that helps us understand it better. The purpose of adding what is actually an extra window to the time domain is to suppress those features of the time domain rectangular window which makes interpretation in the frequency domain more difficult.
When we evaluate the Fourier Transform of what is actually the real signal multiplied by the data window, then the original time domain window, that is the data window, becomes a spectral window (because in the frequency domain we talk about the spectrum of frequencies, or more usually the frequency spectrum). So we are already looking at the frequency spectrum through a spectral window. Mathematically the multiplication in the time domain becomes a convolution in the frequency domain between the actual spectrum and the spectral window. In physical terms the spectral window is the frequency domain filter through which we see the underlying spectrum of the signal. The shape and characteristics of the data window define the nature of the spectral window, or filter, through which we see the frequency spectrum of the original signal.
So the short answer to the question is “yes”, but regretfully we cannot choose the characteristics of the data window and the spectral window independently. There are dozens of different data windows with their corresponding spectral windows, the Hanning window is a good compromise. All useful data windows give spectral windows that tend to be like ideal narrow band filters. This leads to the concept of the Equivalent Noise Band Width (ENBW) measure as one criterion of a good window. Other measures are leakage and bias but that is a tale for another day! Incidentally the best data window measured solely by ENBW is the unavoidable rectangular window, it is the other factors which make it less useful.
Could you please put an example about overlapping technique?
Maybe with the same 10 or 9.5 Hz sinusoidal wave example so that we can see how overlapped window could make a difference in processed frequency spectrum.
SeanL, thanks very much for your question. It got us thinking and John is writing a short article that will make it clearer. We should have the new article available in a week or two. I will post here when it’s ready.
SeanL, John’s reply to your question can be found here – https://blog.prosig.com/2011/08/30/understanding-windowing-and-overlapping-analysis/ Thanks again for the question.
Dear John and Chris,
Thank you for such easy to understand articles. I am learning the vibration analysis technique and your articles are really awesome.