Anytime you measure something which is changing with time, there are multiple ways to quantify the signal. For the purpose of this discussion, we will be talking about how to describe the signal in the time domain.

There are several ways to describe what the time signal is doing. Perhaps the easiest to understand are the Peak and the Peak-to-Peak measures of the signal. These are quite easily understood by looking at the graphical representation of how the signal changes with respect to time. For this purpose, we look at the graphical representation of a simple sinusoid signal.

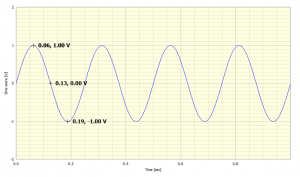
Note that this is a very well behaved and repetitive signal so it is easy to determine the actual values of the signal. It is readily seen that the absolute maximum value (Peak value) of the signal over the measured time is 1.00 Volts (1.00 Vp) and the absolute minimum value of the signal is seen as -1.00 Volts, so the Peak-to-Peak value is 2.00 Volts (2.00 Vpp). In the case of this signal the Mean value is 0 (zero) Volts, but this does not always have to be the case, as is seen in the following example..

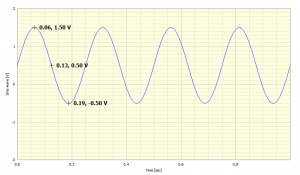
This is the same signal as before, but now it has an offset but with a mean value of 0.5 Volts, The absolute maximum value is 1.50 Volts (1.5 Vp), and the absolute minimum value is -0.50 Volts, so the Peak-to-Peak value is still 2.00 Vpp.

Another measure of signals is called RMS which means root-mean-square of the signal, also known as the quadratic mean. It is a statistical measure of the magnitude of a varying quantity. This measure gives additional information about the signal, namely the “power” of the signal. In more practical terms the RMS Voltage of a time varying signal is the equivalent dc Voltage which yields the same power.

This metric is calculated just as the name implies (RMS means the “root” of the “mean” of the “square” of the values of the signal). First the value of each point of the signal is squared, then these values are averaged over time, and then once this single number is calculated, the square root of this number is the RMS value of the signal. For discrete data points, this is mathematically calculated as:

where is the sequential number of steps in time.

For continuous functions

Where is the time over which the average is taken.

Another metric sometimes used to quantify a signal, although not as frequently, is the average. This is calculated in similar way to how the RMS is calculated, but in this case the signal values are not squared before averaging and the final number is not square rooted.

Looking at examples of how the Peak and Peak-to-Peak values are determined and how the RMS values are calculated shows that the Peak measurements are instantaneous measures whereas the RMS values are average measures. Note that all of the metrics described for quantifying a time signal are totally independent of the period or frequency content of the signal. These calculations can be applied to any time varying signal no matter how complex.

The following two tabs change content below.

• Bio
• Latest Posts

John Mathey

Senior Technical Specialist (Retired) at Prosig

John Mathey graduated with a MS degree from the University of Toledo in 1972. John gained over 35 years of experience with instrumentation, measurement, and analysis. Twenty-five of those years were spent at Ford Motor Company solving and providing training for vehicle noise, vibration, and harshness (NVH) issues. He was a technical specialist at Prosig USA, Inc. where he provided technical support to Prosig customers in the USA. Sadly, John passed away in 2022.

Latest posts by John Mathey (see all)

• Exhaust Vibration Measurement – A Case Study - March 11, 2016
• What Is Amplitude Quantization Error? - January 27, 2016
• Creating An End of Line Vibration Test System - February 25, 2015